Analysis of Planetary Gearsets - Intro
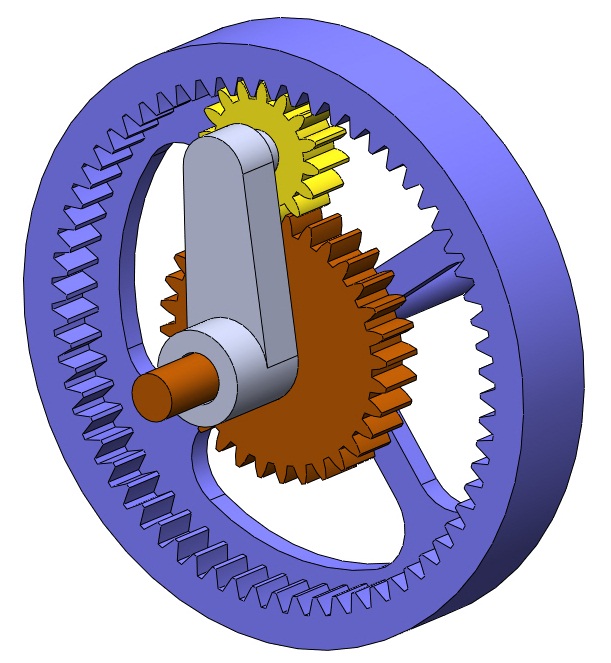
Planetary gearsets can behave in counterintuitive ways, which makes their analysis quite interesting. However, we can develop a few simple formulas which we can apply to any gearset, no matter how complicated. This introductory page is intended to provide some insight into the relationships between the gears in a planetary gearset. Here, I will introduce a table-based method for determining the speed ratios of the simplest kind of planetary gearset, shown in the figure at right. This method was shown to me by Dr. T.R. Chandrupatla, of Rowan University. It is a very useful method for determining relationships for a planetary gearset where one input is fixed. It can be used in the general case (where both inputs have nonzero speed) but is more cumbersome than the formula-based methods shown in the Advanced Analysis page.
The Tabular Method
In the space above you can see a schematic of a basic planetary gearset. Let us assume that the sun has 40 teeth and the planet has 20 teeth. We can easily calculate the number of teeth in the ring by noting that the diameter of the ring is equal to the sun, plus two planets. Therefore
$$N_r=N_s+2N_p=40+2\cdot20=80\text{ teeth}$$Assume that the ring gear is rotating at 100 rpm ccw, and the sun gear is fixed. What is the speed of the carrier?
To solve this, we will first pretend that the carrier is fixed, and will rotate the sun gear (the gear that is fixed in reality). Since the carrier is temporarily fixed, there is no epicyclic motion, and the gears behave like an ordinary gearset. Now, construct the four-column table shown below:
| Sun | Planet | Ring | Carrier | |
|---|---|---|---|---|
| 1 | 1 | -2 | -0.5 | 0 |
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
The first row shows the result of rotating the sun gear by one revolution. The planet gear rotates
$$n_p=-\frac{N_s}{N_p}(1\text{ rev})=-\frac{40}{20}(1\text{ rev})=-2 \text{ rev}$$and the ring gear rotates
$$n_r=\frac{N_p}{N_r}(-2\text{ rev})=-\frac{20}{80}(-2\text{ rev})=-0.5 \text{ rev}$$Note the absence of a minus sign in the second equation, since the ring gear is internal. This motion can be seen in the animation above by clicking on the 'Step 1' button.
| Sun | Planet | Ring | Carrier | |
|---|---|---|---|---|
| 1 | 1 | -2 | -0.5 | 0 |
| 2 | -1 | -1 | -1 | -1 |
| 3 | 0 | -3 | -1.5 | -1 |
| 4 | ||||
| 5 |
Next, we temporarily 'glue' the entire assembly together, and rotate it (as a unit) backwards by one revolution. The backwards rotation is indicated by the row of -1s in row 2 of the table, and the result is shown in row 3. We can justify this step by noting that the relationship between the gears is unaffected by the motion of the gearset as a unit, since this relationship is determined solely by the meshing of the gear teeth. The motion of this step can be seen by clicking on the 'Step 2' button in the animation above.
| Sun | Planet | Ring | Carrier | |
|---|---|---|---|---|
| 1 | 1 | -2 | -0.5 | 0 |
| 2 | -1 | -1 | -1 | -1 |
| 3 | 0 | -3 | -1.5 | -1 |
| 4 | ×-66.6 | ×-66.6 | ×-66.6 | ×-66.6 |
| 5 | 0rpm | 200rpm | 100rpm | 66.6rpm |
Finally, we multiply each column by the number that will make the ring gear spin at 100rpm, as given in the problem statement. In this case, since the ring has spun backwards by 1.5 revolutions, we multiply by -66.6. this final result is shown as rows 4 and 5 in the table. As you can see, when the ring rotates at 100rpm cw, the carrier rotates at 66.6rpm in the same direction. The resulting motion can be seen in the animation below.
Another Example
Let us re-examine the same gearset, but this time we will hold the ring gear fixed, and rotate the sun at 100rpm cw. How fast does the carrier rotate?
For this problem, the fixed gear is the ring, so we first pretend that the carrier is fixed, and rotate the ring one revolution cw. The planet rotates
$$n_p=\frac{N_r}{N_p}(1\text{ rev})=\frac{80}{20}(1\text{ rev})=4 \text{ rev}$$ And the sun rotates $$n_s=-\frac{N_p}{N_s}(4\text{ rev})=-\frac{20}{40}(4\text{ rev})=-2 \text{ rev}$$We enter this information into the first row of the table below.
| Sun | Planet | Ring | Carrier | |
|---|---|---|---|---|
| 1 | -2 | 4 | 1 | 0 |
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
We now "glue" the gearset together, and rotate the frozen unit backwards by one revolution.
| Sun | Planet | Ring | Carrier | |
|---|---|---|---|---|
| 1 | -2 | 4 | 1 | 0 |
| 2 | -1 | -1 | -1 | -1 |
| 3 | -3 | 3 | 0 | -1 |
| 4 | ||||
| 5 |
Finally, the problem statement requires that the sun rotates at 100rpm cw. We multiply row 3 in the table by -33.3 so that the sun column is 100rpm.
| Sun | Planet | Ring | Carrier | |
|---|---|---|---|---|
| 1 | -2 | 4 | 1 | 0 |
| 2 | -1 | -1 | -1 | -1 |
| 3 | -3 | 3 | 0 | -1 |
| 4 | ×-33.3 | ×-33.3 | ×-33.3 | ×-33.3 |
| 5 | 100rpm | -100rpm | 0rpm | 33.3rpm |
The motion of the planetary gearset with sun as input and fixed ring is shown in the animation below.

